Home Linkedin Videos Follow @amunategui ViralML.com


Data Exploration & Machine Learning, Hands-on


"

Recommended free walkthrough, check it out and boost your career:


Boost your data science career

"







Exploring Some Pair-Trading Concepts with Python



Resources

pair trading


Hi there, this is Manuel Amunategui- if you're enjoying the content, find more at ViralML.com



In this post, I want to share some simple ways of comparing stocks that are presumed related. My recommended approach for finding related companies is to use your own domain expertise. The second option is to use a site based on fundamental analysis that shows related companies (Google it, they’re lots out there like tipranks.com). I don’t recommend using pair-trading scanners as you’ll lose your shirt if you aren’t knowledgeable about the stock and sector - trader beware!

Once you have a few stocks in mind, you’re good to continue on with this exercise. Here we will use the ‘pair-trading’ classics of Coca-Cola vs. Pepsi, and FedEx vs. UPS.

Note: Everything discussed here is for educational purposes only.

In [74]:
import glob, os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

Load market data for FDX, UPS, KO, PEP

There are plenty of sources to get free stock market data, Yahoo Finance is one of them. But all those who will want to do some serious research in this area should not rely on free data. You will eventually need a safe, reliable and currated source of stock data - no shortcuts here.

To access current data, you can manually download the files from Yahoo Finance. For example, if you wanted to get the latest historical prices for Apple, simply enter the following link:

https://finance.yahoo.com/quote/FDX/history?p=FDX

And then find and click the "Download Data" link, it will default to one year of end-of-day market data. Run through this process for all four stocks listed in the title and save the four CSV files in a directory named 'data'.

In [71]:
# find the data directory and extract each CSV file
path = "data/"
allFiles = glob.glob(os.path.join(path, "*.csv"))  
np_array_list = []
for file_ in allFiles:
    df = pd.read_csv(file_,index_col=None, header=0)
    # get symbol name from file
    df['Symbol'] = (file_.split('/')[1]).split(".")[0]
    # pull only needed fields
    df = df[['Symbol','Date', 'Adj Close']]
    np_array_list.append(df.as_matrix())
    
# stack all arrays and tranfer it into a data frame
comb_np_array = np.vstack(np_array_list)  
# simplify column names
stock_data_raw = pd.DataFrame(comb_np_array, columns = ['Symbol','Date', 'Close'])
# fix datetime data
stock_data_raw['Date'] = pd.to_datetime(stock_data_raw['Date'], infer_datetime_format=True)
stock_data_raw['Date'] = stock_data_raw['Date'].dt.date

# check for NAs
stock_data_raw = stock_data_raw.dropna(axis=1, how='any')

# quick hack to get the column names (i.e. whatever stocks you loaded)
stock_data_tmp = stock_data_raw.copy()

# make symbol column header
stock_data_raw = stock_data_raw.pivot('Date','Symbol')
stock_data_raw.columns = stock_data_raw.columns.droplevel()
# collect correct header names (actual stocks)
column_names = list(stock_data_raw)

stock_data_raw.tail()
Out[71]:
Symbol FDX KO PEP UPS
Date
2018-07-11 230.22 44.79 112.54 107.33
2018-07-12 232.69 44.67 111.53 108.53
2018-07-13 233.75 44.74 112.69 108.97
2018-07-16 230.18 44.73 112.96 110.65
2018-07-17 231.15 45.25 114.88 111.07
In [72]:
# hack to remove mult-index stuff
stock_data_raw = stock_data_tmp[['Symbol', 'Date', 'Close']]
stock_data_raw = stock_data_raw.pivot('Date','Symbol')
stock_data_raw.columns = stock_data_raw.columns.droplevel(-1)
stock_data_raw.columns = column_names

# replace NaNs with previous value
stock_data_raw.fillna(method='bfill', inplace=True) 

stock_data_raw.tail()
Out[72]:
FDX KO PEP UPS
Date
2018-07-11 230.220001 44.790001 112.540001 107.330002
2018-07-12 232.690002 44.669998 111.529999 108.529999
2018-07-13 233.750000 44.740002 112.690002 108.970001
2018-07-16 230.179993 44.730000 112.959999 110.650002
2018-07-17 231.149994 45.250000 114.879997 111.070000

Make a copy of the data set before transforming it

In [73]:
stock_data = stock_data_raw.copy()

Plot paired stocks on different axes

In [57]:
plt.figure(figsize=(12,5))
ax1 = stock_data['FDX'].plot(color='green', grid=True, label='FDX')
ax2 = stock_data['UPS'].plot(color='purple', grid=True, secondary_y=True, label='UPS')
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()

plt.legend(h1+h2, l1+l2, loc=2)
plt.show()
In [58]:
plt.figure(figsize=(12,5))
ax1 = stock_data['KO'].plot(color='green', grid=True, label='KO')
ax2 = stock_data['PEP'].plot(color='purple', grid=True, secondary_y=True, label='PEP')
h1, l1 = ax1.get_legend_handles_labels()
h2, l2 = ax2.get_legend_handles_labels()

plt.legend(h1+h2, l1+l2, loc=2)
plt.show()

Normalize data

In order to compare moves between differently priced assets, we need to normalize the data.

According to Wikipedia,

In statistics and applications of statistics, normalization can have a range of meanings. In the simplest cases, normalization of ratings means adjusting values measured on different scales to a notionally common scale, often prior to averaging.

https://en.wikipedia.org/wiki/Normalization_(statistics)

Percent Change And Cumsum

A very simple way to do this is to transform price data into percentage changes and apply a rolling sum, known as a cumulative sum.

In [59]:
def normalize_and_accumulate_series(data):
    # take tail to drop head NA
    return data.pct_change().cumsum()

stock_data['FDX'] = normalize_and_accumulate_series(stock_data['FDX'])
stock_data['UPS'] = normalize_and_accumulate_series(stock_data['UPS'])
stock_data['KO'] = normalize_and_accumulate_series(stock_data['KO'])
stock_data['PEP'] = normalize_and_accumulate_series(stock_data['PEP'])

# remove first row with NAs 
stock_data = stock_data.tail(len(stock_data)-1)
In [60]:
stock_data.head()
Out[60]:
FDX KO PEP UPS
Date
2017-07-19 0.008719 0.003582 0.002869 0.010373
2017-07-20 0.004021 0.003359 0.004343 0.006744
2017-07-21 0.006995 0.008044 0.014039 0.007632
2017-07-24 0.007795 0.003825 0.009752 0.002929
2017-07-25 0.015741 0.012745 0.012508 0.012470

Plot paired stocks on same axes

In [61]:
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['FDX'], color='green', label='FDX')
plt.plot(stock_data['UPS'], color='purple', label='UPS')
ax.grid(True)
plt.legend(loc=2)
plt.show()
In [62]:
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['KO'], color='purple', label='KO')
plt.plot(stock_data['PEP'], color='green', label='PEP')
ax.grid(True)
plt.legend(loc=2)
plt.show()

Getting some statistical measurements

In [63]:
# pip install scipy
# pip install statsmodels
from statsmodels.tsa.stattools import coint

def corr(data1, data2):
    "data1 & data2 should be numpy arrays."
    mean1 = data1.mean() 
    mean2 = data2.mean()
    std1 = data1.std()
    std2 = data2.std()
    corr = ((data1*data2).mean()-mean1*mean2)/(std1*std2)
    return corr
In [64]:
stock_name_1 = 'KO'
stock_name_2 = 'PEP'

score, pvalue, _ = coint(stock_data[stock_name_1], stock_data[stock_name_2])
correlation = corr(stock_data[stock_name_1], stock_data[stock_name_2])

print('Correlation between %s and %s is %f' % (stock_name_1, stock_name_2, correlation))
print('Cointegration between %s and %s is %f' % (stock_name_1, stock_name_2, pvalue))

Correlation between KO and PEP is 0.798133
Cointegration between KO and PEP is 0.036950
In [65]:
stock_name_1 = 'UPS'
stock_name_2 = 'FDX'

score, pvalue, _ = coint(stock_data[stock_name_1], stock_data[stock_name_2])
correlation = corr(stock_data[stock_name_1], stock_data[stock_name_2])

print('Correlation between %s and %s is %f' % (stock_name_1, stock_name_2, correlation))
print('Cointegration between %s and %s is %f' % (stock_name_1, stock_name_2, pvalue))

Correlation between UPS and FDX is 0.454536
Cointegration between UPS and FDX is 0.210379

Measuring separatation and spikes highlights

This is straighforward, we simply subtract the two related and normalized series

In [66]:
 
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['FDX'] - stock_data['UPS'], color='purple', label='Diff FDX minus UPS')
ax.grid(True)
ax.axhline(y=0, color='black', linestyle='-') 
plt.legend(loc=2)
plt.show()
In [67]:
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['KO'] - stock_data['PEP'], color='purple', label='Diff KO minus PEP')
ax.grid(True)
ax.axhline(y=0, color='black', linestyle='-') 
plt.legend(loc=2)
plt.show()

Designing spike thresholds

In [40]:
# get the original data set
stock_data = stock_data_raw.copy()
In [41]:
def normalize_series(data):
    # take tail to drop head NA
    return data.pct_change()

stock_data['FDX'] = normalize_series(stock_data['FDX'])
stock_data['UPS'] = normalize_series(stock_data['UPS'])
stock_data['KO'] = normalize_series(stock_data['KO'])
stock_data['PEP'] = normalize_series(stock_data['PEP'])

# remove first row with NAs 
stock_data = stock_data.tail(len(stock_data)-1)
In [42]:
stock_data.head()
Out[42]:
FDX KO PEP UPS
Date
2017-07-19 0.008719 0.003582 0.002869 0.010373
2017-07-20 -0.004697 -0.000223 0.001474 -0.003629
2017-07-21 0.002973 0.004685 0.009696 0.000888
2017-07-24 0.000800 -0.004219 -0.004287 -0.004703
2017-07-25 0.007946 0.008921 0.002756 0.009541
In [48]:
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['FDX'] - stock_data['UPS'], color='purple', label='Diff FDX minus UPS')
ax.grid(True)
ax.axhline(y=0, color='black', linestyle='-') 
ax.axhline(y=0.02, color='red', linestyle='-') 
ax.axhline(y=-0.02, color='red', linestyle='-')
plt.legend(loc=2)
plt.show()
In [47]:
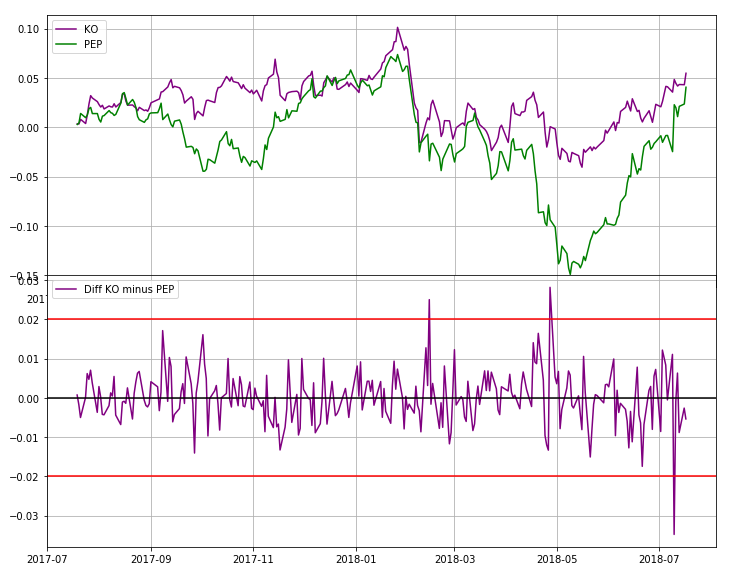
fig, ax = plt.subplots(figsize=(12,5))
plt.plot(stock_data['KO'] - stock_data['PEP'], color='purple', label='Diff KO minus PEP')
ax.grid(True)
ax.axhline(y=0, color='black', linestyle='-') 
ax.axhline(y=0.02, color='red', linestyle='-') 
ax.axhline(y=-0.02, color='red', linestyle='-') 
plt.legend(loc=2)
plt.show()

Manuel Amunategui - Follow me on Twitter: @amunategui